Stop. Think. Check for Confirmation Bias!
Or how homemade graphics of New Zealand mortality rates retweeted round the world are NOT credible.
Confirmation Bias (noun): The tendency to uncritically interpret new evidence as confirmation of one's existing beliefs or theories.
The Beauty (of graphs) is in the Eye of the Beholder.
Time to get another Twitter spat out of my system. Another frustrating experience of spotting mistakes in graphs which much more prominent writers unquestioningly pick up and run with. Some readers will recall my previous run-in with an online educational medical content creator and his inability to recognise obvious errors in reported Texas mortality rate ratios from the official graphed data (The Famous Medical Doctor and the Unknown Twitterer). This time round, I will be exploring why many did not spot the (IMO) obvious inconsistencies in some graphs of New Zealand mortality rates which briefly fired up the online vaccine-skeptical world start of the week. (before the UK ONS data drop started getting all the attention ; )
This post also serves as a chance to revisit the greatest hits of basic statistical fallacies around vaccines from 2021 and will involve basic middle-school math…
Base Rate Fallacy
The first graph which piqued my interest was allegedly freshly released Covid-19 deaths data broken out by both vaccination status age (per age group is always good!):
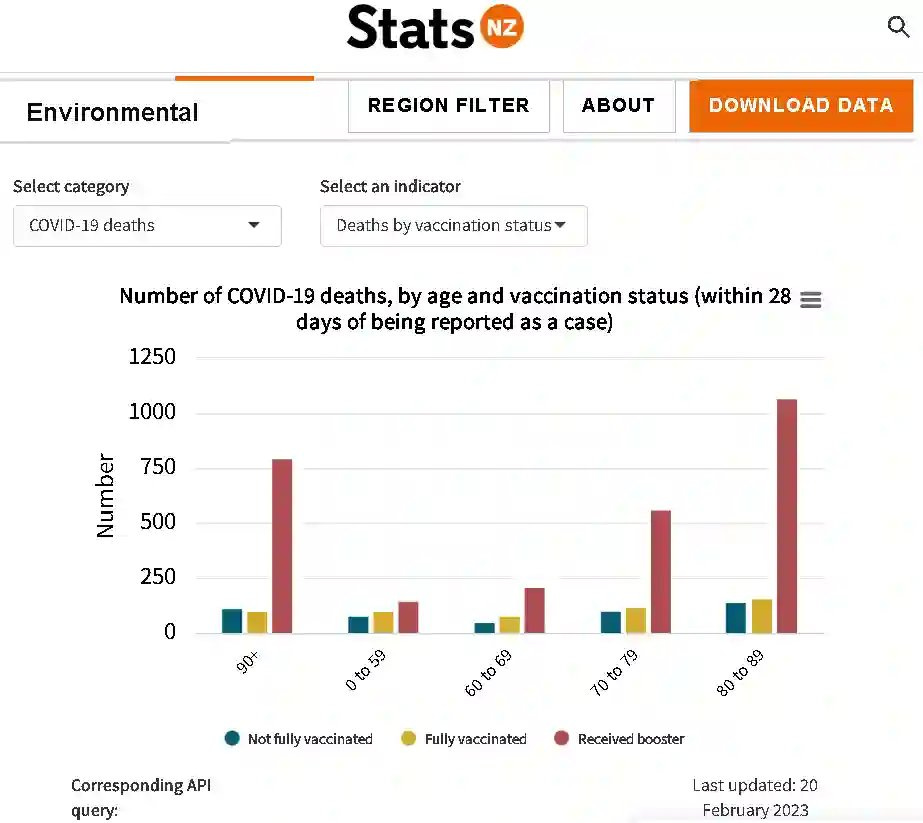
However, the problem with such data, as discussed ad nauseum in 2021, is the counterintuitive phenomenon whereby vaccinated death totals higher than unvaccinated deaths totals is not necessarily indicative of vaccine ineffectiveness. While it may be initially counterintuitive, the logic is simple: If most people in a country are vaccinated and the vaccine does nothing, then, all things being equal (they never are), the percentage of vaccinated people who die will be the same as the percentage of the population vaccinated; If the vaccines are effective, a smaller percentage of deaths will be vaccinated than the percentage of the population vaccinated (positive efficacy); And finally, if the vaccines are really bad, a larger percentage of deaths will be vaccinated than the percentage vaccinated in the overall population (negative efficacy). Therefore, rates (typically per 100K) or even percentages are what count for making valid comparisons. Unfortunately the above graphic shows totals not rates.
(Graphic) Novel Treatments
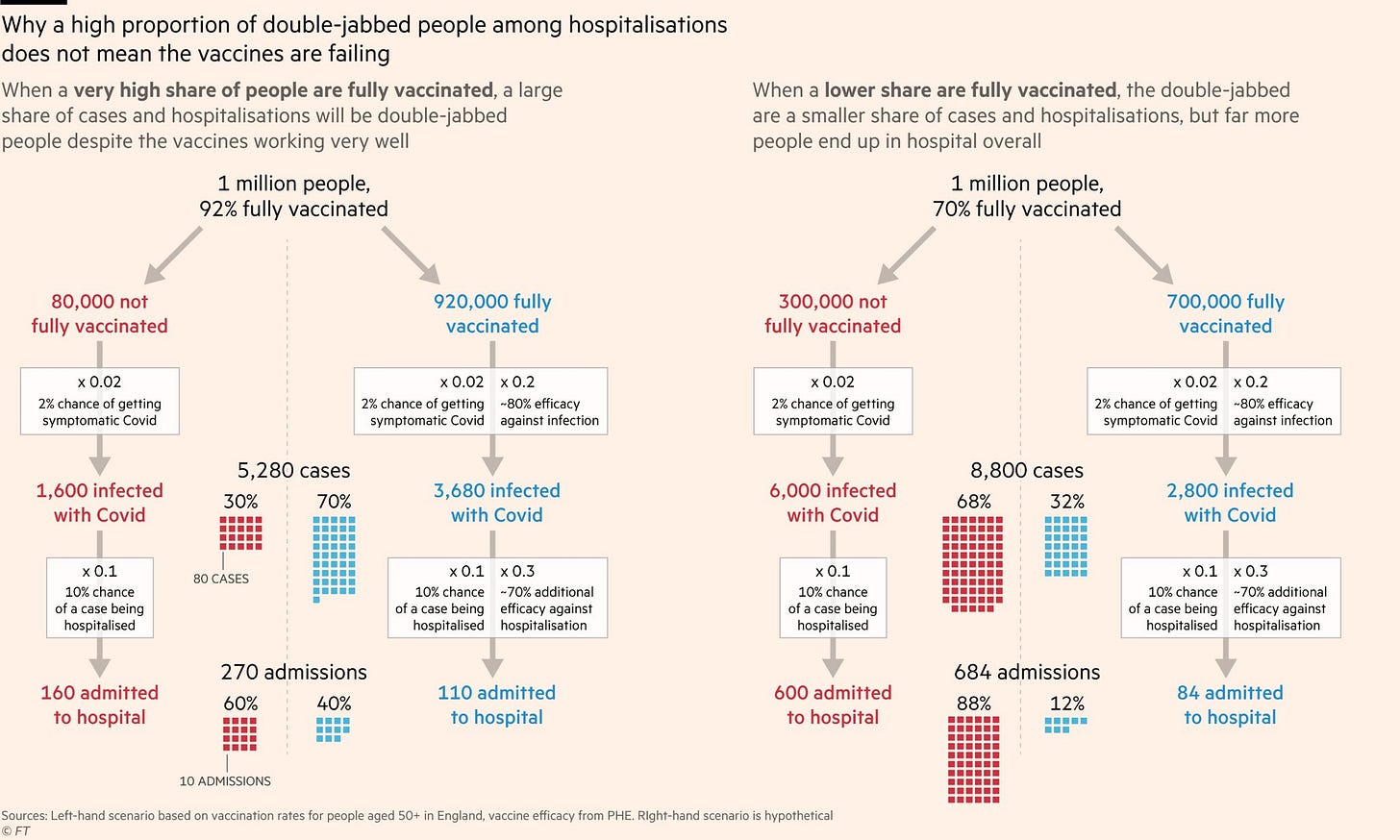
Trying to explain the base rate fallacy around vaccine effectiveness in words doesn’t always work, so the graphic below by James Burn-Murdoch of the Financial Times from 2021 used to be my go-to graphic for sharing way back then. Of course this graphic presumed generous vaccine effectivenss and can do nothing to explain away any trends of increases in totals; for me it simply demonstrates how the (un)expected ratios of outcomes between vaccinated and unvaccinated subgroups of overall populations is dependent on vaccination rates and vaccine efficacy.
Back of the Envelope
As it turns out, the vaccination rates in New Zealand for the older age groups are very high (85~97%) so there is nothing outwardly concerning about the first chart showing much higher Covid-19 deaths in the boostered than in the unvaccinated and double-dosed (once known as “fully vaccinated”). Many will be familiar with vaccine efficacy calculated using incidence rates per 100K:
Vaccine Efficacy = 1 - Rate Ratio
But we can use a simplified formula for vaccine effectiveness which removes the need to know detailed age group population totals and uses the vaccination percentages instead to calculate an Odds Ratio (as opposed to a standard Risk Ratio or Rate Ratio). Taken from a lovely self-study course I found online: Principles of Epidemiology in Public Health Practice - An Introduction to Applied Epidemiology and Biostatistics:
…one of the attractive features of the odds ratio — when the health outcome is uncommon , the odds ratio provides a reasonable approximation of the risk ratio. [Witzbold: death is very uncommon in Covid cases]
Often, the size of the population from which the case-patients came is not known. As a result, risks, rates, risk ratios or rate ratios cannot be calculated from the typical case-control study. However, you can calculate an odds ratio and interpret it as an approximation of the risk ratio, particularly when the disease is uncommon in the population.
Therefore vaccine effectiveness can be approximated using an odds ratio, ie.:
Vaccine Effectiveness ~= 1 - Odds Ratio
[UPDATE: as discussed in comments, this method actually results in exact vaccine effectiveness when comparing two complimentary sub-groups which, when combined, form the total population group, e.g. vaccinated vs unvaccinated]
Doing some back-of-envelope calculations (my old engineering professors loved that phrase and approach) we can estimate vaccine effectiveness against death to determine NZ Covid-19 deaths data is still suggestive of vaccine efficacy of 60~75% for the older age grops depicted in the first chart (using “vaxxed” = “boosted” + “fully vaccinated”). Math WARNING!:
Odds Ratio = (vaxxed:unvaxxed deaths) ÷ (vaxxed:unvaxxed population)
Example - Age group: 60-69
Vaxxed:Unvaxxed Deaths within 28 days = 290:53 = ~5.5 (ie. ~85% deaths vaxxed)
Vaxxed:Unvaxxed Population = 93:7 = ~13.3 (ie. ~93?% population vaxxed)
=>This suggests vaccine effectiveness: 1 - 5.5/13.3 = ~60%
If you don’t like math just recognise that the percentage of Covid deaths which were vaxxed is less than the percentage of population vaccinated.
Show me the data!
The next graphs which caught my eye was this pair:

On the left: the 2022 all-cause monthly death totals by vaccination status provided through a freedom of information (Official Information Act) request to the creator of the graphs. On the right: monthly all-cause mortality Rates per 100K by vaccination status as calculated by the recipient of the FOI data response.
First, there is a notable inflection of boosted vs fully unvaccinated trends in (perhaps unsurprisingly?) both graphs, ie. death totals and death rates. Secondly, and perhaps more remarkbly, the boosted mortality rate rises significantly above the unvaccinated rate after January 2022 and remains so for the rest of the year. Wow! Is this smoking gun evidence of vaccines increasing risk of death? IF true, it’s not just smoking, this is explosive!
Critical Thinking vs Confirmation Bias
If you are a critical thinker, your second thoughts should be: But wait, why has this New Zealand signal of riduculously negative vaccine effectiveness only become apparent now, and why haven’t I seen extremely disproportionate boosted:unboosted mortality rates elsewhere? And how come the Covid-19 deaths data by age group shows positive vaccine effectiveness? Rember, data too good to be true is normally not true! Better to examine the data more closely before trusting the graphs. That’s right, check the data, because that’s what graphs are - data snapshots. Graphs are visual representations of data and they often only offer a limited expression of the fullness of the data.
Simpson’s Paradox Strikes (again!)
The first problem with the paired graphs above, is that the data shown is at an overall population level and is not broken down by age group. Simpson’s Paradox in a nutshell: if an effect or trend is disproportionately found in a subsection of a population, then it may disappear or even be reversed in overall population-level data (and vice-versa)
Over 90% of Covid-associated deaths in NZ occur in the over 60's population (see NZ Covid-19 case demographics here). And around half of All-Cause deaths in NZ occur in over 80's - that is obviously disproportionate. In other words, because Covid-associated deaths (and indeed all deaths) are disproportionately age stratified, it makes no sense to lump masses of healthier, younger persons into overall population level all-cause mortality rates when comparing by vaccination status. It is important to always compare age groups and not overall population groups. At this point it was clear the charts were of limited significance and I tweeted some cautions to those amplifying them.
Did NZ Boosters Boost All-Cause Mortality?
Perhaps, but those graphs above do NOT demonstrate it to be the case. In fairness, it is not instantly recognisable what else is wrong about the above mortality rates without also knowing that these graphs were specifically presented as damning proof of boosters triggering a shift in the trends of mortality rates by vaccination status. The booster rollout in New Zealand certainly correlates strongly with the period of shifting trends:

Shifting Sands of Vaccine Statuses
Leaving aside the delicate matter of when someone freshly vaccinated should be allocated to a new vaccine status group with each new dose (or if they first have to wait in vaccine status limbo for 14 days), calculating any rates by vaccination status for periods during an intensive mass vaccination campaign is not a simple matter. The size of the respective population groups changes on a daily basis as individuals move from one group to the next with each succesive vaccine dose received. This poses the question of which population size is appropriate to use as the denominator when calculating the mortality rates for each age group. And hunting down accurate age-group population sizes and cumulative age-group vaccination rates or group sizes for New Zealand per month of 2022 is also not easy.
Taking a closer look at the values listed on the chart reveals something quite strange. The ratio between the per 100K rates (chart on right) and the actual totals (chart on left) seems to be relatively constant. For example, the number of boosted deaths (chart left) in February is approximately double those for January and correspondingly the boosted mortality rate (chart right) doubles in February. This suggests steady population goup size. BUT how could this be, if the booster campaign was in full swing in Q1 2022? Why do the mortality rates per 100K not reflect the shifting ratios of the different vaccine status groups (boosted:fully-vaccinated:unvaccinated) in the overall population? And why does the boosted mortaliy rate per 100K in January suggest there were already ~2.5 million boostered in January 2022 when the booster campaign only began administering sizable numbers of boosters in December 2021?
Hot Off the Press
Fresh data released through official freedom of information requests is always a little exciting when you get it - I know, I’ve done this myself. It’s kind of a mini-journalistic thrill. You feel like you may have something special on your hands, data that possibly know one else in the public has access to (yet) and you rush to process it and share any insights you can glean from it.
Note, I deliberately haven’t linked to any of the offending tweets or substack posts because this isn’t about the individuals involved. The person who created the graphs seems to be a New Zealand citizen and I am sure she is just as concerned as I am about the experimental vaccines rolled out during the pandemic and the recent rises in all-cause mortality seen in many countries around the world. The same goes for the more prominent tweeters/substackers who unquestioningly amplified her faulty graphs to a much wider audience. According to my Substack stats ~40% of my readers also read some of those writers anyway.
Show Your Work
The thing is, because others don’t have access to the fresh data, it’s important to share (or provide access) to the data so others can verify and check any conclusions you might draw from it. This is the basis of any formal or informal peer review process: cite your sources and starting assumptions, make all data available, and show or explain any work in between to arrive at the final results & conclusions. Indeed, this is the basis of any middle-school science or math class.
Feedback and Corrections
Unable to reconcile the all-cause mortality rates by vaccine status, I reached out on twitter to the creator of the charts explaining that I suspected they had not adjusted the sizes of the different population groups for the ongoing vaccine campaign. I also explained the limitations of the approach lumping younger, healther cohorts with older, higher-risk cohorts when calculating mortality rates by vaccine status for the overall population. I have still received no response.
Then I saw some more charts from the same person again amplified by very prominent twitterers/substackers with mortality rates by age group and vaccination status and I had a brief moment of hope before it became clear the creator was also incorrectly misunderstanding how to correctly calculate rates per 100K by age group.

Age-specific mortality rate: An age-specific mortality rate is a mortality rate limited to a particular age group. The numerator is the number of deaths in that age group; the denominator is the number of persons in that age group in the population.
The ratio between the different age goups in the boosted status is the same in both charts. This could only be the case if the age group population sizes were identical. Unfortunately, the chart creator has apparently used the total boostered population as the denominator when calculating per 100K rates per age group. These charts are thus useless for comparing rates across vaccine statuses.
(Note: I have not investigated the NZ data any further nor have I tried to create corrected charts - I’m not even sure the necessary data is publicly available.)
Check your Confirmation Bias!
In fairness, the substackers did add updates to their posts after receiving pushback from myself and others, though most readers were more than happy to accept their initial conclusions. The more interesting phenomenon is why they so uncritically promoted the (IMO) obviously erroneous charts in the first place. Well, I think the explanation is quite simple - Confirmation Bias.
Confirmation Bias (noun): The tendency to uncritically interpret new evidence as confirmation of one's existing beliefs or theories.
As my friends and readers are well aware, I am also very skeptical about the experimental covid vaccinations and the pandemic hysteria which gripped the world starting 2020 but I still try to apply critical thinking skills to all the data presented to me. Otherwise there is a danger of becoming so wedded to priors that new information can’t break through our cognitive biases.
The Falsification Principle, Karl Popper: The only way to check a hypothesis is to look for all the information that disagrees with it.
A very useful philosophical approach is along the lines of the falsification principle and to try and disprove proposed theories, to consider what information or evidence would cause a change of mind or reappraisal of accepted truths, in order to abandon a favoured hypothesis. It is healthy and necessary to criticise the mainstream narratives but also necessary to guard against reflexively contrarian cognitive biases. If throwing everything at a hyphothesis to try and disprove it fails, and the hypothesis is left still standing, then it increases confidence. But if we are afraid to challenge our beliefs (or when others challenge our beliefs), then we are not really interested in pursuit of the truth.
Summary
To make mistakes is human.
To recognise our mistakes is the start of learning.
To correct our mistakes is the path of growth.
To knowingly spread and promote false information is inacceptable and only undermines the efforts of the entire vaccine-skeptic community.
Stop. Think. Check for Confirmation Bias!
Finally, I agree the trend of increase in all-cause mortality in NZ data does not look good in 2022 :)
Bonus Quote & Video
Would you rather be illusioned or disillusioned?
…would you rather be illusioned or disillusioned? Would you rather have illusions about the world, or would you rather see the way things are? So, to get disillusioned, it’s actually a good thing. The problem for a lot of people in this world,[…] is they, that they identify with something, and when that something then comes under scrutiny they feel personally attacked. Now, to identify with something comes from the Latin word “idem,” which means “the same,” and “facere,” to “make.” So, when you identify, you make yourself the same as something else…
So that when you identify with something, whether for economic or emotional or political or any combination of reasons, and you make yourself the same as that, then when that’s criticized, you’re gonna feel criticized. And so, what I’m saying to people is, don’t afraid to be disillusioned,…
Don’t be afraid to be disillusioned. It’s better to be disillusioned than to be illusioned, and don’t be afraid to be disidentified, you know, don’t identify with something outside of yourself to the extent that you become uncritical and blind.
(The discussion relates somewhat specifically to the identificaiton with and support of Israel by many as a cognitive bias which limits honest discussion and criticism of Israeli government policies but the pyschological principle which the psychotherapist Gabor Maté explains is, in my opinion, universal)
As ever, I appreciate any and all feedback - let me know if you think I have missed something!
And please share my articles if you think others would appreciate them:






This was excellent. You have very clearly shown the base rate fallacy as well as Simpson's paradox. I would suggest, when looking at observational data, the 3rd item to be added to the Mt. Rushmore of biases to examine is the healthy user bias. I believe you comment on my stack so you are not surprised to know that I think this is a critical component to consider in any look at observational data.
This is why we need RCTs. Until yesterday, I was unaware of any RCTs showing a mortality benefit of the vaccines (I have a full-time, unrelated job... keeping up with all of the literature is not possible for me). Someone on Twitter pointed me to a Cochrane paper which, in turn, seemed to rely on a single RC for VE against COVID deaths for Pfizer and Moderna. Hooray! However, when I looked at the papers involved from that RCT, while it claimed VE against severe disease & death was 97%, it also claimed VE against symptomatic infections was >90%. How can I believe the former when the latter is obviously nonsense?
I think you bring your own confirmation bias to the numbers. You ignore the known death rate of unvaccinated in age groups, and Natural immunity gained from previous infections, so if the vax and boosters actually worked then the deaths should be falling not growing in age groups. Especially as the weakest already succumbed to the more "dangerous" variants. Also as the numbers are fudged a little to say people who die within 14 days of a shot arent vaccinated it puts it own skew on the results. Many more professionals are coming to the same conclusion that these jabs do not help, in fact cause infection rate to go higher.